Which agrees with the direct calculation. In calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function f in terms of the derivative of f. Please e-mail any correspondence to Duane Koubaīy clicking on the following address About this document. Your comments and suggestions are welcome. The Chain Rule also has theoretic use, giving us insight into the behavior of certain constructions (as we'll see in the next section).
PROBLEM 21 : Determine a differentiable function y = f( x) which has the propertiesĬlick HERE to see a detailed solution to problem 21.Ĭlick HERE to return to the original list of various types of calculus problems. The Chain Rule allows us to combine several rates of change to find another rate of change. Ĭlick HERE to see a detailed solution to problem 20. If and, determine an equation of the line tangent to the graph of h at x=0. 'Integration by Substitution' (also called 'u-Substitution' or 'The Reverse Chain Rule') is a method to find an integral, but only when it can be set up in a special way. PROBLEM 20 : Assume that, where f is a differentiable function. If g(-1)=2, g'(-1)=3, and f'(2)=-4, what is the value of h'(-1) ?Ĭlick HERE to see a detailed solution to problem 19.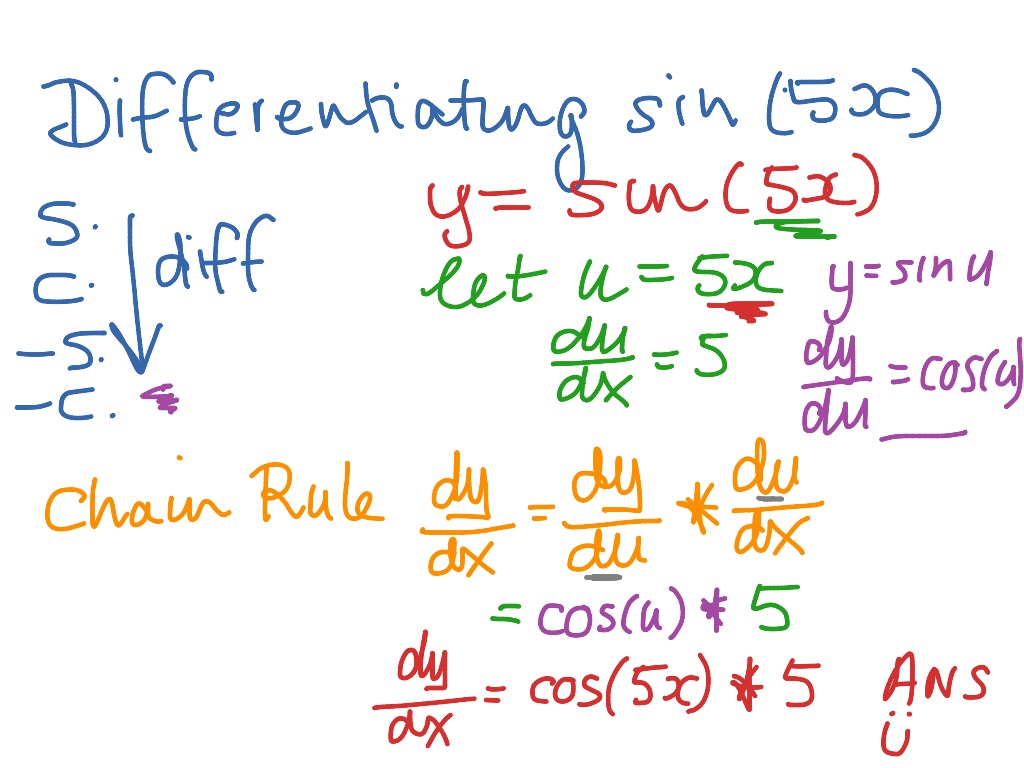 
PROBLEM 19 : Assume that h( x) = f( g( x) ), where both f and g are differentiable functions. The following three problems require a more formal use of the chain rule. The Chain Rule states that the derivative of a composition of at least two different types of functions is equal to the derivative of the outside function f, and then multiplied by the derivative of its inner function g. y ( (1+x)/ (1-x))3 ( (1+x) (1-x)-1)3 (1+x)3 (1-x)-3 3) You could multiply out everything, which takes a bunch of time, and then just use the quotient rule. The following seven problems require more than one application of the chain rule.Ĭlick HERE to see a detailed solution to problem 12.Ĭlick HERE to see a detailed solution to problem 13.Ĭlick HERE to see a detailed solution to problem 14.Ĭlick HERE to see a detailed solution to problem 15.Ĭlick HERE to see a detailed solution to problem 16.Ĭlick HERE to see a detailed solution to problem 17.Ĭlick HERE to see a detailed solution to problem 18. 1) Use the chain rule and quotient rule 2) Use the chain rule and the power rule after the following transformations. In most cases, final answers are given in the most simplified form.Ĭlick HERE to see a detailed solution to problem 1.Ĭlick HERE to see a detailed solution to problem 2.Ĭlick HERE to see a detailed solution to problem 3.Ĭlick HERE to see a detailed solution to problem 4.Ĭlick HERE to see a detailed solution to problem 5.Ĭlick HERE to see a detailed solution to problem 6.Ĭlick HERE to see a detailed solution to problem 7.Ĭlick HERE to see a detailed solution to problem 8.Ĭlick HERE to see a detailed solution to problem 9.Ĭlick HERE to see a detailed solution to problem 10.Ĭlick HERE to see a detailed solution to problem 11. This process will become clearer as you do the problems. 
(the term f'( g( x) ) ), then differentiate the inner layer (the term g'( x) ).
Function f is the ``outer layer'' and function g is the ``inner layer.'' Thus, the chain rule tells us to first differentiate the outer layer, leaving the inner layer unchanged The chain rule is an important derivative rule that allows us to work with composite functions. For example, it is sometimes easier to think of the functions f and g as ``layers'' of a problem. Instead, we invoke an intuitive approach. Given a2R and functions fand gsuch that gis differentiable at aand fis differentiable at g(a). However, we rarely use this formal approach when applying the chain rule to specific problems. THE CHAIN RULE LEO GOLDMAKHER After building up intuition with examples like d dx f(5x) and d dx f(x2), we’re ready to explore one of the power tools of differential calculus.
In the following discussion and solutions the derivative of a function h( x) will be denoted by or h'( x). In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of. The chain rule is a rule for differentiating compositions of functions. The following problems require the use of the chain rule.
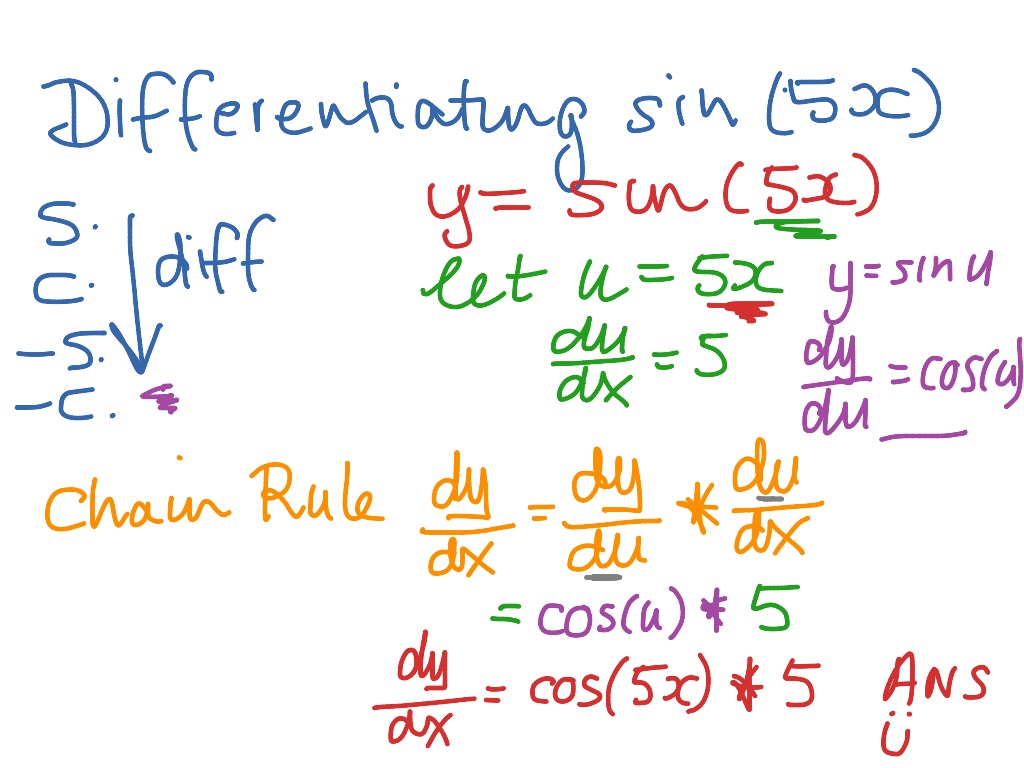
0 kommentar(er)
